转载：Nature: 因果关系可分解为协同、独特和冗余部分
原创作者：Álvaro Martínez-Sánchez, Gonzalo Arranz & Adrián Lozano-Durán
编译：王庆法
麻省理工学院航空航天系学者11月1日在Nature上发表了一篇因果关系的研究文章【文献1】，很有启发性，特此编译介绍。
摘要
因果性是科学探究的核心，作为理解物理系统中变量相互作用的基本依据，即对原因的操控会导致结果的变化。
当前的因果推断方法面临着显著的挑战：包括非线性依赖性、随机交互、自因果作用、汇聚效应以及外部因素的影响等。
本文提出SURD（协同-独特-冗余的因果分解），通过冗余、独特和协同信息的增量来量化因果性，基于过去的观察获得对未来事件的理解。
该方法具有非侵入性，适用于计算和实验研究，即使样本稀缺时也可用。
在因果推断具有显著挑战的场景中，SURD展示出在因果性量化方面比以往方法更高的可靠性。
综述
因果推断有潜力推动多个科学和工程领域的进步，如气候研究、神经科学、经济学、流行病学、社会科学以及流体动力学等。
因果关系必须与关联和相关性这两个概念区分开：关联表示两个变量之间的统计关系，即比随机情况下更频繁地共同出现。
关联并不一定意味着因果，可能源于共同的原因、统计上的巧合或混杂因素的影响。相关性是特殊的关联，度量变量的单调强度和方向。
相关性意味着关联，但不意味着因果；因果关系意味着关联，但不意味着相关性。区分因果性、关联和相关性是一个重大挑战。
因果关系的三个基本构建块是：中介变量、混杂变量和汇聚变量。这些相互作用可以相互交织并存，形成更复杂的因果网络。
考虑三个事件，记为A、B和C：
中介变量（A → B → C）出现在变量A到变量C的因果链中，变量B充当桥梁或中介。中介变量帮助解释独立变量如何影响因变量的潜在机制。
混杂变量（A ← B → C）充当两个变量的共同原因：B → A和B → C。A和C可能通过混杂变量产生统计关联。
汇聚变量（A → B ← C）表示多个因素共同作用于同一个变量：A → B和C → B。大多数变量由于耦合而受到多个原因的影响。
寻找能准确识别中介、混杂和汇聚效应的因果性数学定义仍然是一个活跃的研究领域。
传统方法
因果性的最直观的定义之一依赖于干预的概念：将A修改后观察B中干预后的结果。具有侵入性（修改系统）且成本高昂（重复实验或模拟）。
数据驱动的观察法，如格兰杰因果关系（GC）通过评估自回归模型中引入B变量如何减少A的预测误差来测度从B到A的因果关系。
无模型的因果发现方法，如收敛交叉映射（CCM）及其变体，运用Takens嵌入定理来建立变量与系统吸引子之间的联系。
执行条件独立性检验，如Peter-Clark算法推广，包括瞬时条件独立性检验（PCMCI）最优识别目标变量父节点的简化条件集。
信息论方法
信息论将信息视为物理系统的基本属性，与物理定律的约束和可能性密切相关，也为无模型的因果量化提供了框架。
因果性基于信息与时间箭头之间的紧密联系。系统在宏观层面上存在的时间不对称性可以通过基于香农熵的信息论指标来衡量事件的因果关系。
转移熵（TE）通过了解另一个变量的过去状态来衡量对一个变量未来状态的熵减。条件转移熵（CTE），则是条件GC的非线性、非参数扩展。
其他基于信息论的方法来源于动力系统理论，将因果性量化为由控制方程决定的信息从一个过程流向另一个过程的量。
SURD
当前方法在存在非线性依赖、随机交互（即噪声）、自因果作用、中介、混杂和汇聚效应等情况下仍面临局限。
也无法将因果相互作用分类为冗余、独特和协同，而这对于识别系统中的基本关系至关重要。
SURD：协同-独特-冗余的因果分解，通过冗余、独特和协同贡献来量化因果性，并提供一个衡量隐藏变量因果性的指标。
理论
向量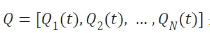
表示N个时间相关变量的集合，Q的各个分量为可观测随机变量。
目标是量化Q的分量对目标变量Qj未来值的因果性，用Qj+=Qj(t+ΔT)表示，其中ΔT>0表示任意时间增量。向量Q可以包含不超过t+ΔT时刻的变量，能够识别滞后和瞬时依赖关系。
SURD 将因果性量化为通过观察Q的个别分量或分量组对Qj+所获得的信息增量（ΔI），Qj+中的信息通过其香农熵H(Qj+)测量。
香农熵可度量不确定性，高熵在其状态被确定时可提供最多的信息。相反，当过程完全确定时，不确定性为零，结果不含额外信息。
利用信息向未来传播的原则（信息仅向未来流动），H(Qj+)可以分解为来自过去和现在的所有因果贡献之和：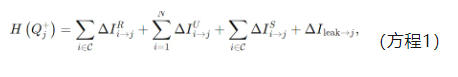
其中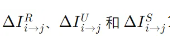
分别表示来自观测变量到Qj+的冗余、独特和协同因果性，而
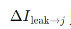则表示来自未观测变量的因果性，称为因果泄漏。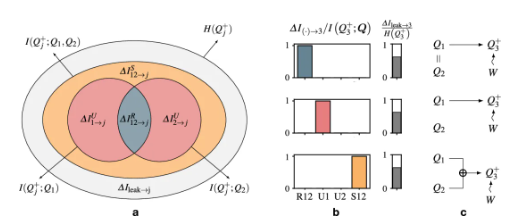
结果
SURD 展现了若干关键特性，有助于通过避免因果性的重复来准确识别相互作用。
方程(1)中的各项均为非负值，并且冗余、独特和协同因果性的总和等于Qj+与Q之间共享的信息，即互信息I(Qj+;Q)。
单个变量Qi与Qj+之间的互信息（记为I(Qj+;Qi)）由涉及Qi的独特和冗余因果性之和表示。
此条件符合因果性来自单一变量至Qj+时仅包含独特和冗余因果性的概念，而协同因果性则源于两个或多个变量的联合效应。
SURD 的信息论公式也非常适合捕捉非线性依赖关系、确定性和随机交互作用，以及自因果性。
方程(1)中的信息正向传播为 SURD 内因果性的归一化奠定了基础。对Qj+的独特、冗余和协同因果性通过I(Qj+;Q)进行归一化，使它们的和等于1。
同样，因果泄漏通过H(Qj+)进行归一化，其值在0到1之间：0 表示Qj+的所有因果性均由Q解释，1 表示Q未解释任何因果性。
验证
我们在多个因果推断面临重大挑战的场景中验证了 SURD。
场景包括具有中介、混杂和协同汇聚效应的系统、Lotka-Volterra 捕食-猎物模型、三种相互作用物种系统、莫兰效应模型、湍流能量级联、湍流边界层的实验数据、由 Sugihara 等人提出的具有时间滞后依赖关系的确定性和随机系统、逻辑门、逻辑映射的同步以及耦合的 Rössler-Lorenz 系统。
中介变量
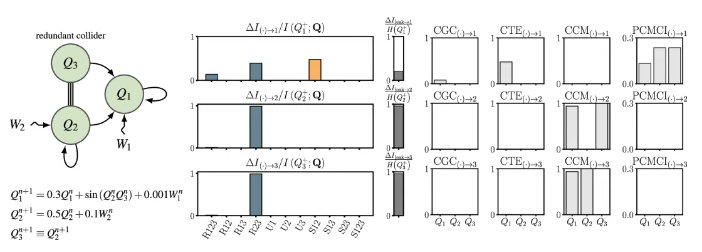
系统Q3→Q2→Q1，其中Q3通过中介变量Q2对Q1产生影响。下图显示了变量之间关系的示意图，以及通过 SURD 和其他因果分析方法得出的结果。
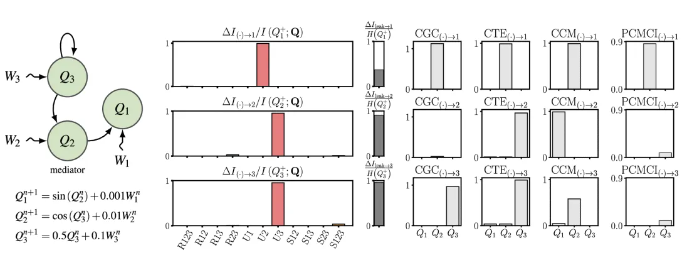
混杂变量
系统中Q3作为Q1 和Q2 的混杂变量，即Q1←Q3→Q2。下图混杂效应的存在在 SURD 中通过协同因果关系来体现，同时发现Q3 的自引因果性。
这突显了 SURD 的另一个优势：因果关系的相对重要性更容易理解，因为它们的归一化值之和总是等于1。
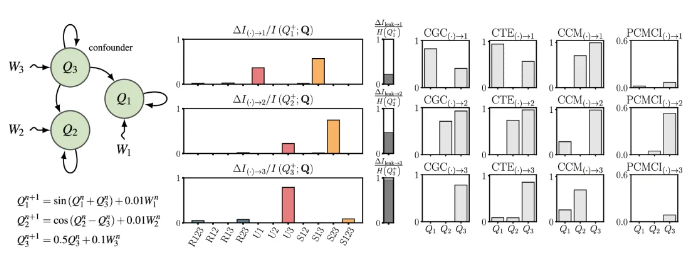
汇聚-协同变量
系统[Q2, Q3]→Q1，其中Q2 和 Q3 共同作用以影响Q1。下图中展示SURD 能够通过协同因果关系检测出Q2和Q3对Q1的主导协同效应，同时还检测到了自引因果性。
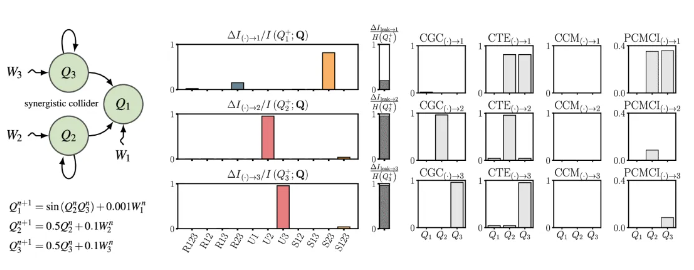
汇聚-冗余变量
基本的交互关系Q2≡Q3→Q1，其中Q3与Q2相同。Q2和Q3对Q1的未来结果有相等的影响。
SURD 识别出与Q2和Q3相关的主要因果关系。Q2 和Q3拥有相同的因果关系（和因果泄漏）表明它们表示相同的变量。
湍流中能量级联的应用
SURD 还可用来研究湍流中能量级联的因果关系：这是一个混沌、多尺度、高维系统的典型例子。
能量级联指的是动能在流动中从大尺度向小尺度（正向级联）或从小尺度向大尺度（逆向级联）的传递。
理解跨尺度的能量传递动力学仍然是一个尚未解决的难题。
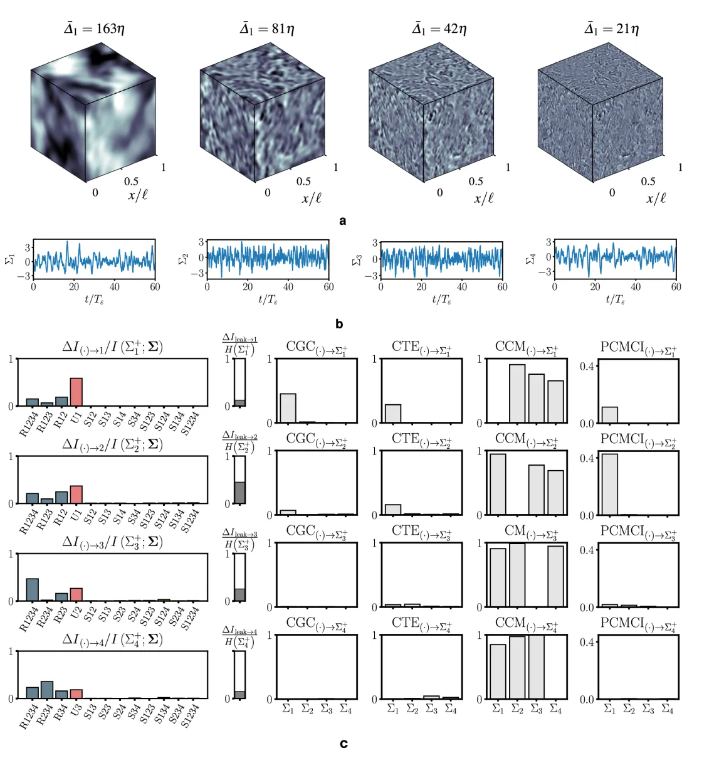
SURD识别了能量传递之间的因果关系。主要贡献来自冗余和独特因果关系，而协同因果关系的作用较小。
独特因果关系（用红色表示）清晰地捕捉到了从大尺度向小尺度的因果能量级联，推导自非零项。
有趣的是，未观察到从小尺度向大尺度的独特因果关系，逆向级联的任何因果关系仅通过冗余关系产生。
讨论
SURD的特性可以归纳为：
适合分析涉及中介、混杂和协同效应的因果网络，这些是变量之间因果交互的基本构建块。
捕捉这些基本交互方面的成功源于区分冗余、独特和协同因果关系的能力，而这一点在以前的方法中缺乏。
确保了所有项的非负性，从而显著增强了可解释性，使得能够清晰地区分变量之间的冗余、独特和协同因果关系。
引入因果泄漏的概念，量化了由于未观察变量而未被考虑的因果关系的程度。
基于转移概率分布，这确保了对变量的平移、缩放和其他一般可逆变换的变换不变性。
总而言之，SURD在因果推断领域中是一种有效工具，有潜力在气候研究、神经科学、经济学、流行病学、社会科学和流体动力学等多个科学和工程领域推动进展。
